Problem Solving With Geometer

Geometer can be used as a powerful aid in finding proofs of theorems and for finding the theorems themselves. This page contains a step-by-step detailed example of the use of Geometer to find and prove a theorem.

If you are interested in practicing this technique on a few moderately difficult problems after reading this, go to the Geometer Problems Page.

Sample Problem

Draw a triangle ΔABC and through each vertex, draw a line parallel to the opposite side of the triangle. This effectively forms three additional triangles congruent to ΔABC on each of its sides.

Inscribe a circle in each of the three new triangles and connect the center of that circle to the opposite vertex of the original ΔABC. These three lines seem to meet at a point. Do they in fact meet there? If so, is it a known point? Can we prove it?

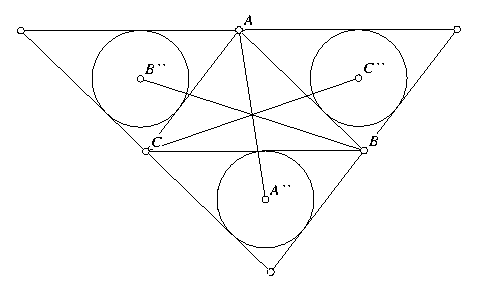
It's probably a good idea to draw this example yourself in Geometer, but if you are lazy, you can download the file Problem.T. After drawing or downloading the example, move the vertices A, B, and C and note that the three lines from A, B, and C to the centers of the opposite inscribed circles seem to meet at a point.

Even if you drew the figure yourself, to follow along it's probably better to download the Problem.T file above so that the labels, et cetera, will agree with the text below.

Here is the diagram you should see:

Testing the Hypothesis

The first thing you can easily check is whether the lines meet to the accuracy of the computer; perhaps they miss by an amount smaller than a pixel or your eyes are just not too good. To do this first test of your hypothesis, load Problem.T into Geometer and in the Proof pull-down menu, select the option Test Diagram. Now jiggle around points A, B, and C a little, and then select the End Text option from the same Proof pull-down menu. A window will appear that looks something like this:

This is file: I:\html\geometer\Test\relations.txt

Concurrent lines:
    (AA'') (CC'') (BB'') 
Concurrent lines:
    (BC) (AC) (l9) (CC'') 
Concurrent lines:
    (AB) (AC) (l7) (AA'') 
Concurrent lines:
    (AB) (BC) (l8) (BB'') 
Equal angles:
    (B A C) (A B v4) (A C v5) (C v6 B) (C v6 v4) (B v6 v5) 
    (v4 v6 v5)

...together with lots of other stuff. What's important is the fist line that indicates that, at least to the accuracy of the computer, the lines AA'', BB'' and CC'' seem to meet at a point in every configuration of the diagram that appeared while you moved the vertices A, B, and C. This is pretty good evidence that the lines are, in fact, concurrent.

Note: The way to scroll in the Relations window is to click in it with the mouse and use the up-arrow and down-arrow keys.

Identifying the Point

Warning: This section is slightly advanced; especially with respect to Geometer usage. You will not miss too much if you skip it.

If you know anything about triangle centers (like the incenter, circumcenter, orthocenter, centroid, et cetera), this point looks like one. To see if it is one of the more common centers, you can use the Geometer diagram Finder.T that comes with the standard release.

If you don't have the standard release, download Finder.T here.

Load Finder.T into Geometer and you will see a triangle with vertices A, B, and C. You need to construct your possible new center on this triangle.

To save time, here is how I would do it:

Set the "Line Type" to "Line"; this will make all your lines go forever in both directions.
Double-click on the "VL=>L Par" command. This will let you repeatedly click on a vertex and a line and draw the line parallel to that line through the vertex. Then click on A followed by the segment BC, then B followed by AC, then C followed by AB. Finally, click on the "Cancel Repeat Mode" button to get out of repeat mode.
Under the Primitives/Circle pull-down, hold down the "Ctrl" key while you select the option LLL=>C. This will let you click on the three edges of a triangle to draw the circle tangent to all three (the incircle). Do this three times to make the three circles. Click on the "Cancel Repeat Mode" button to get out of this mode.
Under the Primitives/Vertex pull-down, hold down the "Ctrl" key while you select the option C=>V Ctr. This generates the point at the center of a circle if you click on the circle. Do this three times to get the centers you want, and then cancel repeat mode.
Now connect the vertices of the triangle to the circle centers appropriately, and find the intersection of two of those lines. Change the color of that final vertex to "Cyan".
Click on one of the lines you created and set the color to "Invisible". Now click on the "Set Color" button and start clicking on all the lines, circles, and points you drew except for the final one that is in the color Cyan. Click on the "Cancel Repeat Mode" button to get out of this mode.
Finally, under the Edit pull-down, select the option Edit Geometry. Go to the end of the file where the line for the final vertex should contain text that looks like: [.cyan, .in]. Edit this text to be: [.cyan]. Use the "Save File" (or Ctrl-S) option to save the file. At this point, your diagram should look just like it started, but with one new cyan-colored point that is the purported triangle center.

Now, to see if your point is a well-known triangle center, press the "N" key (or "Next" button). A bunch of triangle centers will appear. If one of them seems to match your point, wiggle the vertices A, B, and C, and check to see if it tracks your point. This should not happen the first time.

If there are no matches, press "N" again to look at another batch of centers. Continue in this way until you either exhaust the centers, or find a point that seems to match. In this case, you should find that your point is the same as the so-called "Speiker Center". If you look that up, you'll see that it is the incenter of the triangle formed by connecting the midpoints of the sides of the original triangle.

You may want to test this on the original figure in the diagram Problem.T. In that figure, find the midpoints of the triangle sides, form a triangle by connecting them, find the inscribed circle, and finally, find its center. That point should agree with the intersection of the lines. AA'', BB'', and CC''. If you do this, quit the diagram without saving your work and reload the original Problem.T if you wish to continue the next section.

Knowing that your point is the Speiker Center may or may not help solve the problem, but at least it is interesting information.

Looking for a Proof

Let's see if we can show that the lines are concurrent. If you play with the diagram a bit, it probably looks like the lines AB and A''B'' are parallel (also that AC is parallel to A''C'' and BC is parallel to B''C'') . (This is pretty obvious, but let's pretend for a second that it is not.)

We can again check, at least to the accuracy of the computer, by drawing the line A''B'' and running the Test Diagram-End Test commands as we did earlier. If we do that, among lots of other information, we obtain these interesting lines: (Remember that you can scroll in the Relations window is to click in it with the mouse and use the up-arrow and down-arrow keys.)

Parallel lines:
    (AB) (l5) (l9) (B''A'')

and

Equal length segments:
    [A B] [C v5] [C v6] [B'' A'']

This indicates that not only are the lines AB and A''B'' parallel, but they are the same length! That means that the quadrilateral AB''A''B is a parallelogram, and we know that the diagonals of a parallelogram bisect each other.

If we can show that, then we're basically done, since clearly BC will be parallel to and equal to B''C'', et cetera. Since we can form three different parallelograms using different pairs, each set of diagonals bisect each other, so all three must meet at the same point which is the midpoint of AA'', of BB'', and of CC''.

So how do we show that AB is parallel to A''B''? Well, A'' and B'' are the centers of circles tangent to the line through C parallel to AB, so they are the same distance from it (all three circles are of equal diameter, since all the three newly-created triangles are easily shown to be congruent). Thus A''B'' is parallel to a line known to be parallel to AB, so A''B'' is parallel to AB.

How do we show that AB = A''B''? Well, if we label the leftmost point in the diagram above X and the bottommost point Y, then since ΔXAC is congruent to ΔCBY, and B'' and A'' lie on the angle bisectors of all the angles of those triangles, we know that ∠XAB'' = ∠CBA'', so AB'' || A''B. Thus AB''A''B is a parallelogram and we are done.

Contact Information:

Tom's Home Page
Geometer Home Page

Email Tom: tomrdavis@earthlink.net.